Comparative study of machine learning methods for carbon metering in power generation enterprises

Carbon measurement modeling workflow

Figure 1 below presents the overall workflow of the carbon measurement modelling for power generation enterprises proposed in this study. The entire method consists of three core stages. The first stage is the data preparation stage, where actual operational data from power generation enterprises is analyzed. Eighteen characteristic parameters, including power generation volume, fuel type, and load rate, are integrated, and the most predictive key factors are selected using a feature selection strategy. The second stage is the model construction stage, where three different machine learning algorithms are compared, and targeted hyperparameter optimization is implemented for each model to enhance its performance. The final stage is the evaluation and output stage, where the model’s prediction accuracy is comprehensively verified through the evaluation of RMSE, MAE, R², and MAPE. The optimal model is then verified to support the enterprise’s carbon management, energy conservation, and emission reduction decisions. This structured workflow design ensures the traceability and reproducibility of the entire process from raw data to decision support.

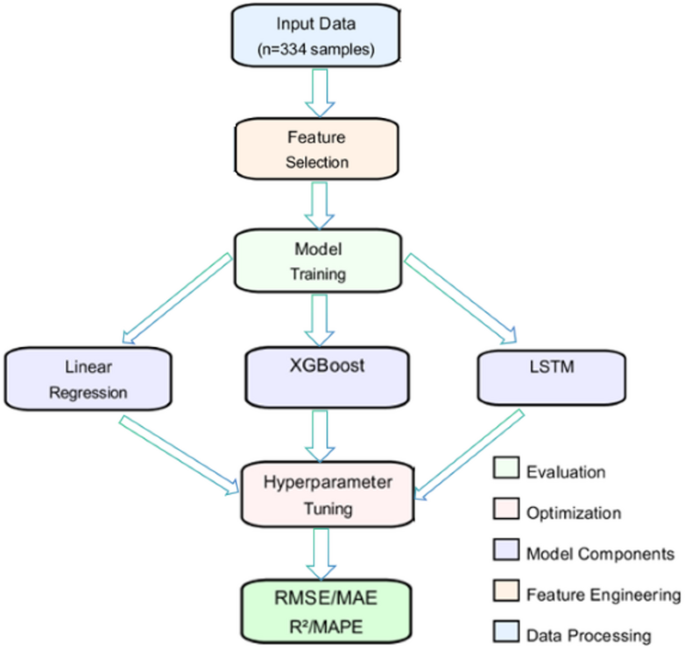
The overall workflow of carbon measurement modeling for power generation enterprises.

Feature selection strategy

(1) Correlation-driven feature selection.

By analyzing the statistical correlation between features and target variables, this method selects the features that contribute significantly to the prediction target. Its core methods include:

Pearson Correlation Coefficient: It primarily measures the linear correlation between features and target variables, and is suitable for scenarios where the data distribution is close to normal and the relationship exhibits a linear trend. For example, in power load forecasting, a linear correlation often exists between temperature and electricity consumption, and key features can be quickly identified using the Pearson coefficient. Its limitation is that it cannot capture non-linear or non-monotonic relationships.

Spearman Rank Correlation: By comparing rank differences between features and target variables (i.e., ranking differences), the monotonic non-linear correlation between the two is assessed. For example, equipment ageing and failure rates may show a non-linear but monotonically increasing trend, in which Spearman’s coefficient is more advantageous than Pearson’s. This method is robust to outliers, but can not identify complex wave-type relationships.

(2) Model-based feature importance assessment.

Model-based feature importance assessment. The contribution of features to output variables is quantified by constructing a prediction model. The specific methods include:

Tree-based ensemble learning importance score:

XGBoost, Random Forest and other algorithms are used to calculate the contribution value of feature splitting, including gain contribution, feature frequency and coverage feature splitting.

Permutation Importance:

The importance of features is evaluated by randomly disrupting eigenvalues and measuring the degree of performance degradation of the model. This method is particularly suitable for identifying key predictors in time series data.

(3) System implementation of recursive feature elimination (RFE).

Recursive Feature Elimination (RFE) is a top-down feature selection method that gradually removes the least important features through an iterative optimization process. In each iteration, the model’s performance is evaluated using k-fold cross-validation, and a curve of feature number versus model performance is constructed to determine the optimal feature subset. The early stop mechanism is introduced in the feature screening process to prevent excessive screening from degrading model performance.

In summary, through this series of systematic feature selection methodologies, the carbon emission prediction model can extract the most predictive feature subset from the massive number of features, significantly improving the prediction accuracy and model generalization ability.

Machine learning method selection and its principle

This study selects three machine learning algorithms, namely multi-source linear regression, XGBoost, and long short-term memory network (LSTM), to construct carbon emission prediction models. The selection is mainly based on the following comprehensive considerations: aiming to cover the complete methodological spectrum from basic linear models to complex nonlinear ensemble models and then to deep time series models, in order to systematically evaluate the applicability of different modeling paradigms. Specifically, multi-source linear regression provides a benchmark for understanding the potential linear relationship between features and carbon emissions and has high interpretability; XGBoost, with its strong ability to capture nonlinear patterns and efficient handling of feature interactions, is suitable for analyzing the complex relationships formed by multiple factors in the power generation process; while LSTM is specifically used to explore possible time series dependencies in carbon emission data, and its gating mechanism can effectively model dynamic processes. This diversified model combination not only reflects the mainstream methods in the current field of carbon emission prediction but also directly serves the core goal of this study to identify the optimal prediction model and support enterprises in achieving precise carbon management and emission reduction decisions.Now let’s start introducing the specific principles of each method one by one:

Multi-source linear regression.

Multiple linear regression is used to describe the relationship between the independent variable (explanatory variable) and the dependent variable (response variable) by establishing a linear equation. Multi-source linear regression is suitable for the case where the relationship between data features is relatively linear, and the calculation is simple and easy to explain.

where, Y = [y₁,y₂,…,y_n]^T, represent the carbon emission vector (n = 334);

\({\mathbf{X}}=\left[ {\begin{array}{*{20}{c}} {{x_{11}}}& \cdots &{{x_{1p}}} \\ \vdots & \ddots & \vdots \\ {{x_{n1}}}& \cdots &{{x_{np}}} \end{array}} \right]\), is the feature matrix (p = 18);

β = [β₀,β₁,⋯ ,β_p]^T, is the regression coefficient.

XGBoost

XGBoost (eXtreme Gradient Boosting) is an ensemble learning algorithm. The objective function comprises a loss function (mean squared error) and a regularization term to balance the model’s complexity and generalization ability. The loss function, that is, the negative gradient of the current model, is used as an approximation of the residual, and then a new decision tree is fitted to predict the residual. The process is iterated until the preset stopping condition is met, thereby gradually improving the model’s performance.

where \(l({y_i},{\hat {y}_i})\) is the loss function and \({\text{\varvec{\Omega}}}({f_k})\) is the regularization term.

LSTM

LSTM ( Long-Short Term Memory, LSTM ) is a special recurrent neural network ( RNN ). By learning long-term dependencies through memory and forgetting mechanisms, input sequence data (such as carbon emissions from the past few days, electricity demand, etc.) is used, and the forgetting gate, input gate, and output gate of the LSTM unit are utilized to update the hidden state, ultimately predicting future carbon emissions.

Forget gate :

Input gate :

Candidate memory units :

Cell state update :

Output gate :

The final hidden state :

where, \(\sigma\) Represents the sigmoid activation function (output [0, 1]), \({{\mathbf{h}}_{t – 1}}\) represents the hidden state at the previous moment, \({{\mathbf{x}}_t}\) is the current input feature, \({{\mathbf{W}}_o}\), \({{\mathbf{W}}_i}\), \({{\mathbf{W}}_{\text{c}}}\), \({{\mathbf{W}}_f}\) are weight matrices, \({{\mathbf{b}}_i}\), \({{\mathbf{b}}_o}\), \({{\mathbf{b}}_f}\)represent bias vectors, \({{\mathbf{C}}_{t – 1}}\) is the cell state at the previous moment, tanh is the hyperbolic tangent activation function, \({{\mathbf{\tilde {C}}}_t}\) is the current cell state, \({{\mathbf{i}}_t}\) controls the storage intensity of new information\({{\mathbf{\tilde {C}}}_t}\), \({{\mathbf{o}}_t}\) is the proportion of the cell state output externally, \({{\mathbf{h}}_t}\)is the final output temporal feature representation.。.

To address the temporal dependencies in carbon emissions of power generation enterprises, the LSTM architecture employs a forget gate\({{\mathbf{f}}_t}\) to preserve long-term factors such as fuel quality stability, while the input gate \({{\mathbf{i}}_t}\) captures short-term fluctuations including load variations. The cell state\({{\mathbf{\tilde {C}}}_t}\) integrates the full operational cycle status of generating units. Subsequently, the output gate\({{\mathbf{o}}_t}\) generates a hidden representation adapted to key dynamic features (X1, X3, X10, X11). This representation is ultimately mapped to daily carbon emission predictions through a linear transformation layer.

Indicators for model evaluation

Root mean square error (RMSE)

RMSE represents the standard deviation of the error between the predicted value and the actual value, and has the same unit as the original data. It can directly reflect the absolute deviation scale between the predicted value and the actual value。.

Mean absolute error (MAE)

MAE is the average absolute value to measure the difference between the predicted value and the actual value. It is less sensitive to outliers and is suitable for intuitive evaluation of the average error level. By calculating the average value of the absolute error, the interference of outliers on the evaluation results is reduced, and the overall average error level of the model can be stably reflected.

Coefficient of determination (R²)

The index to measure the goodness of fit of the model indicates the proportion of variance explained by the model relative to the total variance. The value range of R² is [0,1], the value of R² is closer to 1, the better the model fitting effect is.By quantifying the proportion of the model’s interpretation of the total variance of carbon emissions, it directly reflects the model’s ability to capture the correlation between complex factors in the power generation process and carbon emissions.

Mean absolute percentage error (MAPE)

MAPE can measure the average percentage of the difference between the predicted value and the actual value, and the results are expressed as a percentage, which facilitates comparison of different models or data sets.It helps to compare the prediction accuracy of different models, and at the same time can directly convey the error level to enterprise managers, providing a clear reference basis for carbon management decisions.

Model optimization

Considering that the model’s accuracy may be further optimized, this section discusses the hyperparameter tuning strategy of the model. The specific tuning strategies of each model are as follows :

Linear regression model: its parameters are directly solved by the least squares method, which does not involve the iterative optimization process.

XGBoost model: In the tuning strategy for the XGBoost model, three critical parameters—denoted as the hyperparameter set θ={η,d, n}—are optimized via grid search. Learning rate (η): Candidate values{0.01,0.1,0.2}.Max tree depth (d): Candidate values{3,5,7}. Number of trees (n): Candidate values{50,100,200}. The optimization objective is to minimize the validation loss (RMSE) over the

where \({D_{val}}\) is the validation dataset, and \({f_\theta }\) is the XGBoost model parameterized by θ.

LSTM model: The optimization process for the LSTM model primarily targets the input sequence length, denoted as s, which represents the number of consecutive historical days used to predict the next day’s carbon emissions. Other model parameters, such as the hidden dimension, number of layers, dropout rate, and training hyperparameters (e.g., learning rate, batch size), remain fixed at preset values. The candidate values for the sequence length are s ∈ {5, 7, 10}, selected to capture short-term (5 days), weekly (7 days), and medium-term (10 days) temporal patterns.

Input sequence: Given a time step t, the input sequence Xt(s) is a matrix comprising feature vectors from day t − s + 1 to day t:

where x_τ ∈ R^d is the feature vector at day τ, and s is the sequence length.

Prediction target: the LSTM model f_LSTM maps the input sequence Xt(s) to the predicted carbon emission \({\hat {y}_{t+1}}\)for the next day (t + 1):

Here, ϕ denotes the fixed parameters of the LSTM architecture.

The optimal sequence length ∗s∗ is determined by minimizing the root mean square error (RMSE) on the validation set via time-series cross-validation:

where RMSE_val(s) is computed as:

where \({\mathcal{D}_{{\text{val}}}}\) is the validation set, and \(\hat {y}_{{t+1}}^{{(s)}}\) is the prediction for day t + 1 generated by the LSTM model trained with sequence lengths.